SQL Lessons

In January I did not travel anywhere. My biggest thrills were seeing the musical Cats and having a physical exam. Therefore, I don't have one of my great travel stories to start off this column. Instead, I am going to teach you some SQL tricks.

In case you need to refresh your memory about relational databases, the ACM is publishing past articles of computing laureates under a "Classic of the Month" project. In November, it published E.F. Codd's original paper on a relational approach to data a nd normalization ("A Relational Model of Data for Large Shared Data Banks," 1970). The ACM's Internet address is: http://www.acm.org.

Answering Ralph Kimball's Challenge

With my ego, how can I let a challenge like that go unanswered? Go back and get your January and February issues of DBMS (or order them and make my publisher very happy), so you can follow along. Let's start with the simple Sales table shown in Listing 1. The values in the table are pretty random, but they will do for now. Ralph's first example in February was a report with the sale date, the amount, a running total (sequenced by dates), and a three-day moving average of the sales amount. In the days befo re scalar subqueries, this would indeed have been impossible, but now I can use one scalar subquery for each of the statistics in the problem:

SELECT saledate, amount,
 (SELECT COUNT(DISTINCT saledate)
  FROM Sales AS S1
  WHERE S0.saledate >= S1.saledate) AS day_number,
 (SELECT SUM(amount)
  FROM Sales AS S2
  WHERE S0.saledate >= S2.saledate) AS cum_total,
 (SELECT AVG(amount)
  FROM Sales AS S3
  WHERE S3.saledate
   BETWEEN S0.saledate - INTERVAL 2 DAYS
   AND S0.saledate) AS three_day_avg
 FROM Sales AS S0;

SELECT saledate, amount, qty,
 (amount/qty) AS unit_price,
 (SELECT SUM(amount)/SUM(qty)
  FROM Sales AS S2
  WHERE S0.saledate >= S2.saledate) AS
   cum_unit_price,
 (SELECT (SUM(amount)/SUM(qty))/ 3.0
  FROM Sales AS S3
  WHERE S3.saledate
   BETWEEN S0.saledate-2 AND S0.saledate) AS
    three_day_avg 
 FROM Sales AS S0;

SELECT saledate, amount,
 (SELECT SUM(amount)
  FROM Sales AS S1
  WHERE S0.amount >= S1.amount) AS cum_total,
 (CASE
  WHEN cum_total <= (SELECT SUM(amount) FROM
   Sales)/3.0
  THEN 'Low' WHEN cum_total >= 2'(SELECT SUM(amount)
   FROM Sales)/3.0
  THEN 'High'
  ELSE 'Medium'
  END) AS tertile
FROM Sales AS S0
ORDER BY amount;

As an aside, I disagree with Ralph about the definition of a ranking. I was taught that when values are the same (or tied), they both get the same rank and the next element in the sequence gets the next number; the lack of gaps in the sequence is useful in other statistics. Ralph stated that when values are tied, they both get the same rank, but the next element in the sequence skips a number for each element in the tie. I learned to call this second approach a "standing" because it is used to determine class standings in the British school system. You can simply change the "COUNT (DISTINCT x)" to "COUNT (x)" in my code to get a standing.

Some of the other examples Ralph gave are reports, not queries. That means that they have two or more different types of rows in them, which violates closure -- you cannot use them as subqueries or expressions in other queries. The reports are also sorte d, which is not part of a SQL query. The ORDER BY clause in SQL is part of a cursor statement, not part of a query. In the SQL standard, the ORDER BY clause is the closest thing there is to a report writer.

Now, having said all of this, I need to add one more thing: Don't use the queries I just showed you on a data warehouse! Use a report writer or OLAP tool designed for your warehouse. My sample queries are portable, standard SQL, but they will not finish running within the memory of living man on most implementations.

ANSI and ISO are working on a standard for an Ada-like procedural language for triggers and stored procedures that should be complete by the time you read this column. Perhaps SQL should add a report writer module, similar to Cobol. But that is a topic f or another column.

Nested Set Model of Trees, Part 2

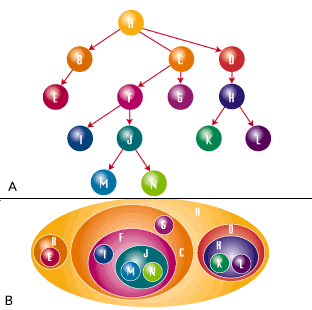
The tree in Figure 1 is represented as A) a graph and B) nested sets. Therefore, it can be navigated in only one direction along its edge. The direction is shown by the nesting; that is, you know that someone is the subordinate of someone else in the company hierarchy because that person's left and right set numbers are between those of their bosses. The same thing is true of the adjacency matrix model, but it represents the direction of the edge with columns that have the start a nd finish nodes.

Another property I did not mention last time is that the children are ordered; that is, you can use the set numbers to order the children from left to right. This is not true of the adjacency matrix model, which has no ordering among the children. You sh ould consider this fact when you are inserting, updating, or deleting nodes in the tree.

A defining property of a tree is that it is a graph without cycles. That is, no path folds back on itself to catch you in an endless loop when you follow it in the tree. Another defining property is that there is always a path from the root to any other node in the tree. In the nested set model, paths are shown as nested sets, which are represented by the nested set's numbers and between predicates. For example, to find out all the managers to whom a particular worker reports in the company hierarchy, y ou would write:

SELECT 'Mary',
P1.emp, (P1.rgt - P1.lft) AS size
FROM Personnel AS P1, Personnel AS P2
WHERE P2.emp = 'Mary'
AND P2.lft BETWEEN P1.lft AND P1.rgt;

Mary	emp	size
====	===	====
Mary	Albert	27
Mary	Charles	13
Mary	Fred	9
Mary	Jim	5
Mary	Mary	1

Notice that when the size is equal to one, you are dealing with Mary as her own boss. If you don't allow employees to think for themselves, you may want to exclude this case.

The nested set model uses the fact that each containing set is larger in size (size is defined as right to left) than the sets it contains. Obviously, the root will always have the largest size. JOINS and ORDER BY clauses do not interfere with the nested set model like they do with the adjacency graph model. Plus, the results are not dependent on the order in which the rows are displayed. Users of Oracle tree extensions should be aware of this advantage.

The level of a node is the number of edges between it and a path back to the root. You can compute the level of a given node with the following query:

SELECT P2.emp, COUNT(*) AS level
FROM Personnel AS P1, Personnel AS P2
WHERE P2.lft BETWEEN P1.lft AS P2
GROUP BY P2.emp;

This query finds the levels of bureaucracy among managers, as follows:

emp	level
===	=====
Albert	1
Bert	2
Charles	2
Diane	2
Edward	3
Fred	3
George	3
Heidi	3
Igor	4
Jim	4
Kathy	4
Larry	4
Mary	5
Ned	5

In some books on graph theory, you will see the root counted as level zero instead of level one. If you like that convention, use the expression "(COUNT(*)-1)" instead.

The self-join and BETWEEN predicate combination is the basic template for other queries. In particular, you can use views based on the template to answer a wide range of questions. In fact, this month's puzzle involves a few of thos e questions.

Aggregate Functions on Trees

SELECT P1.emp, SUM(P2.salary) AS payroll
FROM Personnel AS P1, Personnel AS P2
WHERE P2.lft BETWEEN P1.lft AND P1.rgt
GROUP BY P1.emp;

emp	payroll
===	=======
Albert	7800.00
Bert	1650.00
Charles	3250.00
Diane	1900.00
Edward	750.00
Fred	1600.00
George	750.00
Heidi	1000.00
Igor	500.00
Jim	300.00
Kathy	100.00
Larry	100.00
Mary	100.00
Ned	100.00

Deleting Subtrees

DELETE FROM Personnel
WHERE lft BETWEEN
(SELECT lft FROM Personnel WHERE emp = :downsized)
AND
(SELECT rgt FROM Personnel WHERE emp = :downsized);

The problem is that this query results in gaps in the sequence of nested set numbers. You can still perform most tree queries on a table with such gaps because the nesting property is preserved. That means you can use the between predicates in your queri es, but other operations that depend on the density property will not work in a tree with gaps. For example, you will not find leaf nodes by using the predicate (right-left=1), nor will you find the number of nodes in a subtree by using the left and righ t values of its root.

Unfortunately, you just lost some information that would be very useful in closing those gaps -- namely the right and left numbers of the subtree's root. Therefore, forget the query and write a procedure instead:

CREATE PROCEDURE DropTree (downsized IN CHAR(10) NOT NULL)
BEGIN ATOMIC
DECLARE dropemp CHAR(10) NOT NULL;
DECLARE droplft INTEGER NOT NULL;
DECLARE droprgt INTEGER NOT NULL;

Now save the dropped subtree data with a single select:

SELECT emp, lft, rgt
INTO dropemp, droplft, droprgt
FROM Personnel
WHERE emp = downsized;

The deletion is easy:

DELETE FROM Personnel
WHERE lft BETWEEN droplft and droprgt;

Now close up the gap:

UPDATE Personnel

SET lft = CASE

WHEN lft > droplf

THEN lft - (droprgt - droplft + 1)

ELSE lft END,

rgt = CASE

WHEN rgt > droplft

THEN rgt - (droprgt - droplft + 1)

ELSE rgt END;END;

Deleting a Single Node

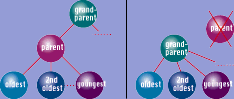
The second method for deleting a single node in the middle of a tree is to connect the children to the parent of the original node (say Mom dies and the kids are adopted by Grandma, as shown in Figure 3). This happens automatically in the nested set model; you simply delete the node and its children are already contained in their ancestor nodes. However, you must be careful when you try to close the gap left by the deletion. There is a difference in renumbering the descendants of the deleted node and renumbering other nodes to the right. Following is a procedure for doing so:

CREATE PROCEDURE DropNode (downsized IN CHAR(10) NOT NULL)
BEGIN ATOMIC
DECLARE dropemp CHAR(10) NOT NULL;
DECLARE droplft INTEGER NOT NULL;
DECLARE droprgt INTEGER NOT NULL;

Now save the dropped node data with a single select:

SELECT emp, lft, rgt

INTO dropemp, droplft, droprgt

FROM Personnel

WHERE emp = downsized;

DELETE FROM Personnel
WHERE emp = downsized;

And now close up the gap:

UPDATE Personnel

SET lft = CASE

WHEN lft BETWEEN droplft AND droprgt THEN lft - 1

WHEN lft > droprgt THEN lft - 2

ELSE lft END

rgt = CASE

WHEN rgt BETWEEN droplft AND droprgt THEN rgt - 1

WHEN rgt > droprgt THEN rgt -2

ELSE rgt END;

WHERE lft > droplft;

END;

Puzzle

1. Find all the subordinates of an employee.
2. Find all the common bosses of two employees (this is a query for "cousins" in a family tree).
3. All I had in the original declaration of the Personnel table was one constraint (lft<rgt); can you think of more constraints that would help ensure a correct table? (See Puzzle Answer.)

LISTING 1

CREATE TABLE Sales

(saledate DATE NOT NULL PRIMARY KEY,

qty INTEGER NOT NULL,

product CHAR(3) NOT NULL,

amount DECIMAL (8,2) NOT NULL);

INSERT INTO Sales VALUES ('1996-02-01', 13, 'A', 1000.00);
INSERT INTO Sales VALUES ('1996-02-02', 12, 'B', 900.00);
INSERT INTO Sales VALUES ('1996-02-03', 10, 'B', 950.00);
INSERT INTO Sales VALUES ('1996-02-04', 10, 'C', 914.25);
INSERT INTO Sales VALUES ('1996-02-05', 10, 'C', 750.00);
INSERT INTO Sales VALUES ('1996-02-06', 7, 'B', 810.00);
INSERT INTO Sales VALUES ('1996-02-07', 7, 'A', 753.00);
INSERT INTO Sales VALUES ('1996-02-08', 6, 'C', 800.75);
INSERT INTO Sales VALUES ('1996-02-09', 6, 'A', 500.00);
INSERT INTO Sales VALUES ('1996-02-10', 5, 'A', 102.54);
INSERT INTO Sales VALUES ('1996-02-11', 5, 'A', 100.00);
INSERT INTO Sales VALUES ('1996-02-12', 3, 'B', 145.67);
INSERT INTO Sales VALUES ('1996-02-13', 3, 'A', 100.12);
INSERT INTO Sales VALUES ('1996-02-14', 1, 'A', 184.13);
INSERT INTO Sales VALUES ('1996-02-15', 1, 'B', 172.98);

LISTING 2

CREATE TABLE Personnel

(emp CHAR (10) PRIMARY KEY,

salary DECIMAL (8,2) NOT NULL CHECK (salary >= 0.00),

lft INTEGER NOT NULL,

rgt INTEGER NOT NULL,

CHECK (lft < rgt));

INSERT INTO Personnel VALUES ('Albert', 1000.00, 1, 28);
INSERT INTO Personnel VALUES ('Bert', 900.00, 2, 5);
INSERT INTO Personnel VALUES ('Charles', 900.00, 6, 19);
INSERT INTO Personnel VALUES ('Diane', 900.00, 20, 27);
INSERT INTO Personnel VALUES ('Edward', 750.00, 3, 4);
INSERT INTO Personnel VALUES ('Fred', 800.00, 7, 16);
INSERT INTO Personnel VALUES ('George', 750.00, 17, 18);
INSERT INTO Personnel VALUES ('Heidi', 800.00, 21, 26);
INSERT INTO Personnel VALUES ('Igor', 500.00, 8, 9);
INSERT INTO Personnel VALUES ('Jim', 100.00, 10, 15);
INSERT INTO Personnel VALUES ('Kathy', 100.00, 22, 23);
INSERT INTO Personnel VALUES ('Larry', 100.00, 24, 25);
INSERT INTO Personnel VALUES ('Mary', 100.00, 11, 12);
INSERT INTO Personnel VALUES ('Ned', 100.00, 13, 14);

Figure 1.

Figure 2.

Figure 3.

Puzzle Answer

SELECT M1.emp, ' manages ', Subordinates.emp
FROM Personnel AS M1, Personnel AS Subordinates
WHERE Subordinates.left BETWEEN M1.left AND M1.right;

2. First create a view, which will be useful later:

CREATE VIEW ReportsTo (emp, boss)
AS SELECT P2.emp, P1.emp
FROM Personnel AS P1, Personnel AS P2
WHERE P2.lft BETWEEN P1.lft AND P1.rgt;

Then, use the following query to obtain the chain of command for one employee, keeping only the bosses he/she has in common with the other employees:

SELECT :firstguy, :secondguy, boss
 FROM ReportsTo
 WHERE emp = :firstguy
 AND boss IN (SELECT boss
  FROM ReportsTo
  WHERE emp = :secondguy);

CREATE TABLE Personnel
 (emp CHAR (10) PRIMARY KEY,
 salary DECIMAL (8,2) NOT NULL CHECK (salary >=
  0.00),
 lft INTEGER NOT NULL UNIQUE CHECK(lft > 0),
 rgt INTEGER NOT NULL UNIQUE CHECK(rgt > 0),
 CHECK (lft < rgt));