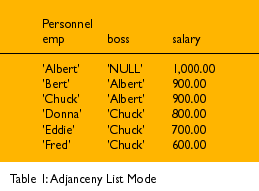
This theme is an old one of mine, but it is worth repeating. I have been seeing too many questions about SQL trees and hierarchies in the newsgroup discussions. The usual example of a tree structure in SQL books is called an adjacency list model and it looks like this:
CREATE TABLE Personnel (emp CHAR(10) NOT NULL PRIMARY KEY, boss CHAR(10) DEFAULT NULL REFERENCES Personnel(emp), salary DECIMAL(6,2) NOT NULL DEFAULT 100.00);

Another way of representing trees is to show them as nested sets. Because SQL is a set-oriented language, this model is a better than the usual adjacency list approach you see in most textbooks. Let us define a simple Personnel table like this, ignoring the left (lft) and right (rgt) columns for now:
CREATE TABLE Personnel (emp CHAR(10) NOT NULL PRIMARY KEY, lft INTEGER NOT NULL UNIQUE CHECK (lft > 0), rgt INTEGER NOT NULL UNIQUE CHECK (rgt > 1), CONSTRAINT order_okay CHECK (lft < rgt) );
This problem is always given with a column for the employee and one for his boss in the textbooks. This table (Table 2) -- without the lft and rgt columns -- is called the adjacency list model, after the graph theory technique of the same name; the pairs of nodes are adjacent to each other.

The organizational chart would look like Figure 1 as a directed graph:
Figure 1
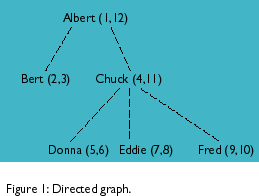
Table 1 is denormalized in several ways. We are modeling both the personnel and the organizational chart in one table. But for the sake of saving space, pretend that the names are job titles and that we have another table that describes the personnel that hold those positions.
Another problem with the adjacency list model is that the boss and employee columns are the same kind ( names of personnel) and therefore should be shown in only one column in a normalized table. To prove that this is not normalized, assume that "Chuck" changes his name to "Charles;" you have to change his name in both columns and several places. The defining characteristic of a normalized table is that you have one fact in one place at one time.
The final problem is that the adjacency list model does not model subordination. Authority flows downhill in a hierarchy, but if I fire Chuck, I disconnect all of his subordinates from Albert. There are times (such as water pipes) where this is true, but that situation is not expected in this case.
To show a tree as nested sets, replace the nodes with ovals, then nest subordinate
ovals inside each other. The root will be the largest oval and will contain
every other node. The leaf nodes will be the innermost ovals with nothing else
inside them and the nesting will show the hierarchical relationship. The rgt
and lft columns (I cannot use the reserved words LEFT and RIGHT
in SQL) are what show the nesting.
If that mental model does not work, then imagine a little worm crawling counter-clockwise along the tree. Every time it gets to the left or right side of a node, the worm numbers it. The worm stops when it gets all the way around the tree and back to the top.
This model is a natural way to show a parts explosion, because a final assembly is made of physically nested assemblies that break down into separate parts.
At this point, the boss column is both redundant and denormalized, so it can be dropped. Also, note that the tree structure can be kept in one table and all the information about a node can be put in a second table, and you can join both on employee number for queries.
To convert the graph into a nested sets model think of a little worm crawling along the tree. The worm starts at the top -- the root -- and makes a complete trip around the tree. When it comes to a node, it puts a number in the cell on the side that it is visiting and increments its counter. Each node will get two numbers -- one for the right side and one for the left. (Computer Science majors will recognize this as a modified preorder tree traversal algorithm.) Finally, drop the unneeded "Personnel.boss" column, which represents the edges of a graph.
This has some predictable results that we can use for building queries. The
root is always of the form (left = 1, right = 2 * (SELECT COUNT(*) FROM
TreeTable)); leaf nodes always have (left + 1 = right); the BETWEEN
predicate defines the subtrees; and so on. Here are some common queries that
you can use to build others:
1. Find an employee and all his/her supervisors, no matter how deep the tree.
SELECT P2.*
FROM Personnel AS P1, Personnel AS P2
WHERE P1.lft BETWEEN P2.lft AND P2.rgt
AND P1.emp = :myemployee;
2. Find the employee and all his/her subordinates. (This query has a nice symmetry with the first query.)
SELECT P2.*
FROM Personnel AS P1, Personnel AS P2
WHERE P1.lft BETWEEN P2.lft AND P2.rgt
AND P2.emp = :myemployee;
3. Add a GROUP BY and aggregate functions to these basic queries
and you have hierarchical reports. For example, the total salaries that each
employee controls:
SELECT P2.emp, SUM(S1.salary)
FROM Personnel AS P1, Personnel AS P2,
Salaries AS S1
WHERE P1.lft BETWEEN P2.lft AND P2.rgt
AND P1.emp = S1.emp
GROUP BY P2.emp;
In the adjacency list method, this has to be done with a cursor.
4. Find the level of each node, so you can print the tree as an indented listing.
SELECT COUNT(P2.emp) AS indentation, P1.emp FROM Personnel AS P1, Personnel AS P2 WHERE P1.lft BETWEEN P2.lft AND P2.rgt GROUP BY P1.emp ORDER BY P1.lft;
5. The nested set model has an implied ordering of siblings that the adjacency list model does not. To insert a new node as the rightmost sibling:
BEGIN
DECLARE right_most_sibling INTEGER;
SET right_most_sibling
= (SELECT rgt
FROM Personnel
WHERE emp = :your_boss);
UPDATE Personnel
SET lft = CASE WHEN lft > right_most_sibling
THEN lft + 2
ELSE lft END,
rgt = CASE WHEN rgt >= right_most_sibling
THEN rgt + 2
ELSE rgt END
WHERE rgt >= right_most_sibling;
INSERT INTO Personnel (emp, lft, rgt)
VALUES ('New Guy', right_most_sibling,
(right_most_sibling + 1))
END;
6. To convert an adjacency list model into a nested set model, use a push down stack algorithm. Assume that we have these tables:
-- Tree holds the adjacency model
CREATE TABLE Tree
(emp CHAR(10) NOT NULL,
boss CHAR(10));
INSERT INTO Tree
SELECT emp, boss FROM Personnel;
-- Stack starts empty, will holds the nested set model
CREATE TABLE Stack
(stack_top INTEGER NOT NULL,
emp CHAR(10) NOT NULL,
lft INTEGER,
rgt INTEGER);
BEGIN ATOMIC
DECLARE counter INTEGER;
DECLARE max_counter INTEGER;
DECLARE current_top INTEGER;
SET counter = 2;
SET max_counter = 2 * (SELECT COUNT(*) FROM Tree);
SET current_top = 1;
INSERT INTO Stack
SELECT 1, emp, 1, NULL
FROM Tree
WHERE boss IS NULL;
DELETE FROM Tree
WHERE boss IS NULL;
WHILE counter <= (max_counter - 2)
LOOP IF EXISTS (SELECT *
FROM Stack AS S1, Tree AS T1
WHERE S1.emp = T1.boss
AND S1.stack_top = current_top)
THEN
BEGIN -- push when top has subordinates, set lft value
INSERT INTO Stack
SELECT (current_top + 1), MIN(T1.emp), counter, NULL
FROM Stack AS S1, Tree AS T1
WHERE S1.emp = T1.boss
AND S1.stack_top = current_top;
DELETE FROM Tree
WHERE emp = (SELECT emp
FROM Stack
WHERE stack_top = current_top + 1);
SET counter = counter + 1;
SET current_top = current_top + 1;
END
ELSE
BEGIN -- pop the stack and set rgt value
UPDATE Stack
SET rgt = counter,
stack_top = -stack_top -- pops the stack
WHERE stack_top = current_top
SET counter = counter + 1;
SET current_top = current_top - 1;
END IF;
END LOOP;
END;
Although this procedure works, you might want to use a language that has arrays in it, instead of trying to stick to pure SQL.
Joe Celko is an Atlanta-based independent consultant. He is the author of Instant SQL Programming (Wrox Press, 1997). You can contact him at www.celko.com or 71062.1056@compuserve.com.